澳门六合彩彩票网博彩平台存款_

在代码蓄意中鄙俗靠近这样的场景，给定两个元素，咱们需要快速判断他们是否属于归并个聚会，同期不同的聚会在需要时还能快速合并为一个聚会，举例咱们要开采一个随意期骗，那么判断两个用户是否是一又友关联，大致两东说念主是否属于归并个群就需要用到咱们咫尺提到的功能。

皇冠最新网址

这些功能看似简便，但有个难点在于你要解决的“填塞快”，假定a,b两个元素差别属于聚会A,B,判断它们是否属于归并个聚会的平直作念法即是遍历聚会A中总计元素，望望是否能找到b，若是聚会A中包含n个元素，那么该作念法的时间复杂度即是O(n)，当聚会元素许多，况且判断的次数也许多时，这样的作念法效力就会很低，本节咱们要望望能不成找到次线性的算法。

咱们先看复杂度为O(n)的算法逻辑，假定咱们有6个元素，编号差别为0到6，咱们不错使用部队来模拟聚会，属于归并个聚会的元素就存储在归并个部队中，然后每个元素通过哈希表映射到部队头，如下图所示：

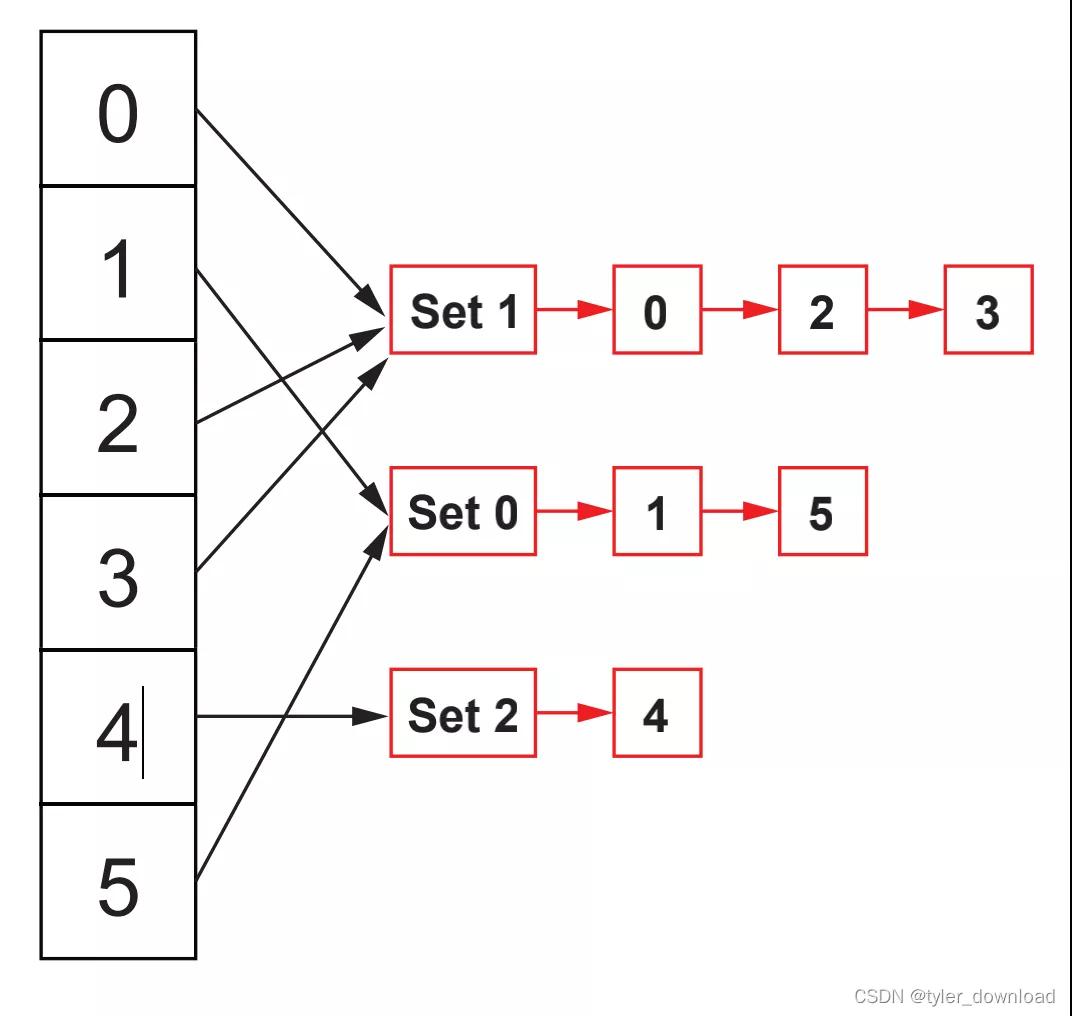
在这种数据结构下，查询两个元素是否属于归并个聚会，那么惟有通过哈希表找到各自元素场地部队的头部，判断头部是否一致即可，咱们用areDisjoint(x,y)来默示两个元素是否属于一个聚会，那么在刻下数据结构下areDisjoint的时间复杂度是O(1)。

皇冠,足球,面条

若是要合并两个元素场地聚会，咱们用merge(x,y)来默示，那么在刻下结构下，咱们惟有找到x和y对应的部队头部，然后从x场地部队的头部遍历到终末一个元素，然后将终末一个元素的next指针实行y场地的部队头部，如下图所示：

澳门六合彩彩票网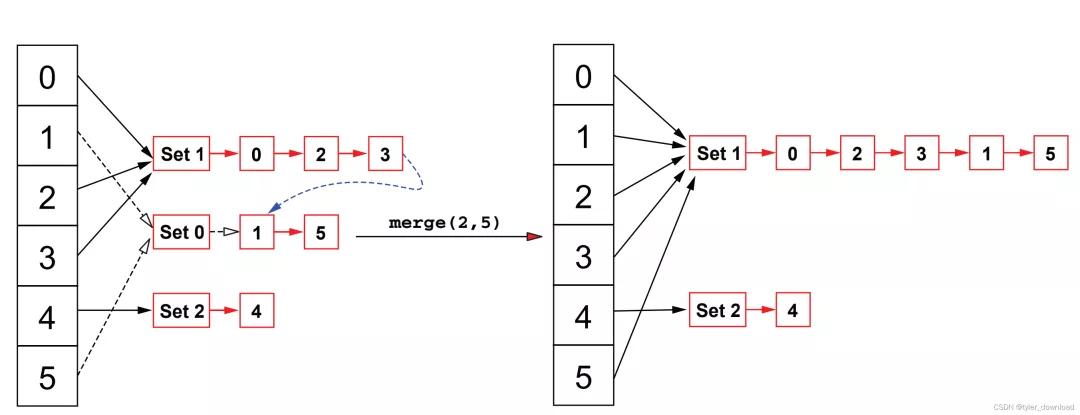

皇冠盘abcd盘

同期咱们还需要作念一个操作，那即是修改第二个聚会中每个元素映射的部队头部，因此在刻下结构下，merge(x,y)对当令间复杂度为O(n)，因为从部队头遍历到末尾是O(n),同期遍历y场地聚会每个元素，修改他们映射的部队头，时间复杂度亦然O(n)。

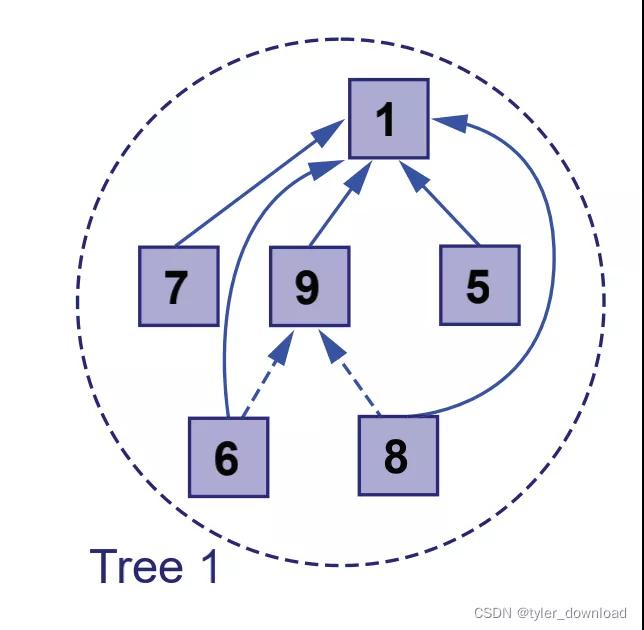
咫尺问题是咱们能否将合并所需要的时间进行优化。咱们防护到合并时有两个措施很耗时，一是从部队走到队尾，二是修改第二个聚会中每个元素指向的部队头。是以耗时其实是因为咱们使用部队来默示聚会所导致。为了优化时间，咱们将部队换成多叉树，如下图所示：

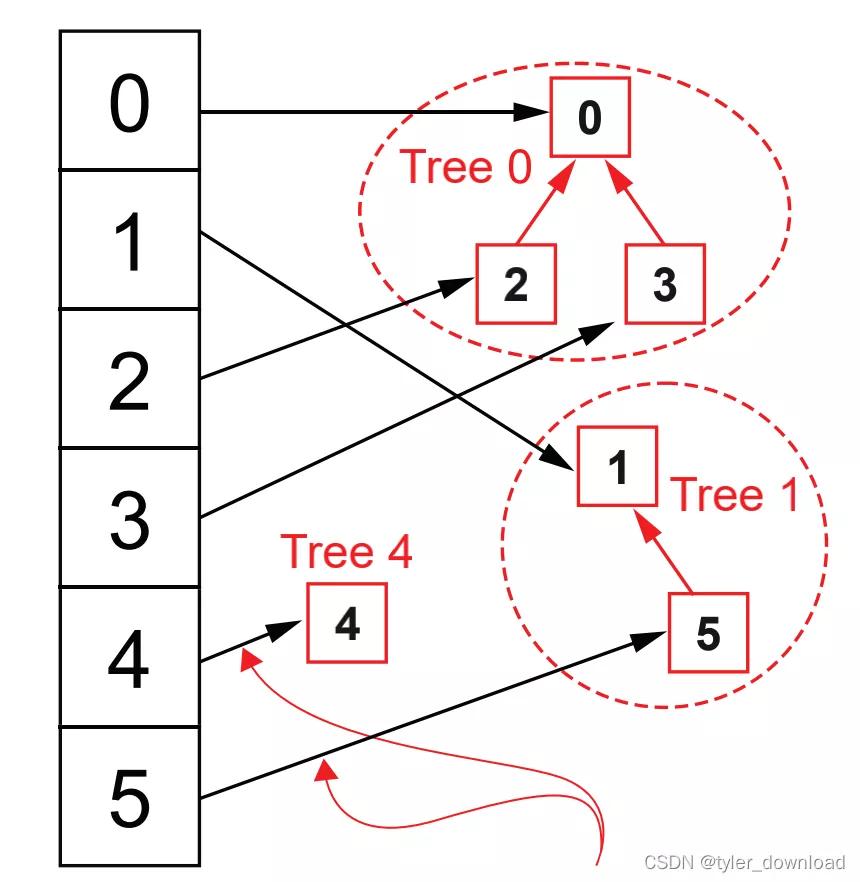
此时咱们不再使用哈希表来将元素映射到部队头部，而是将归并个聚会的元素安插到归并个多叉树中，要判断两个元素是否属于归并聚会，咱们惟有沿着元素的父节点指针往上走一直找到树的根节点，若是找到交流的根节点，那么两个元素就属于归并聚会，关于排序二叉树而言，树的高度为O(lg(n))，n是树的节点数，于是判断两个元素是否属于归并聚会所需时间复杂度为O(lg(n))。

当需要合并两个元素关于的聚会时，咱们差别找到两个元素关于的根节点，然后将高度较低的那棵树的根节点行为高度较高那棵树的子节点，这个解决对效力很紧迫，后头咱们会进一步磋磨，树合并的情形如下图所示：

博彩平台存款

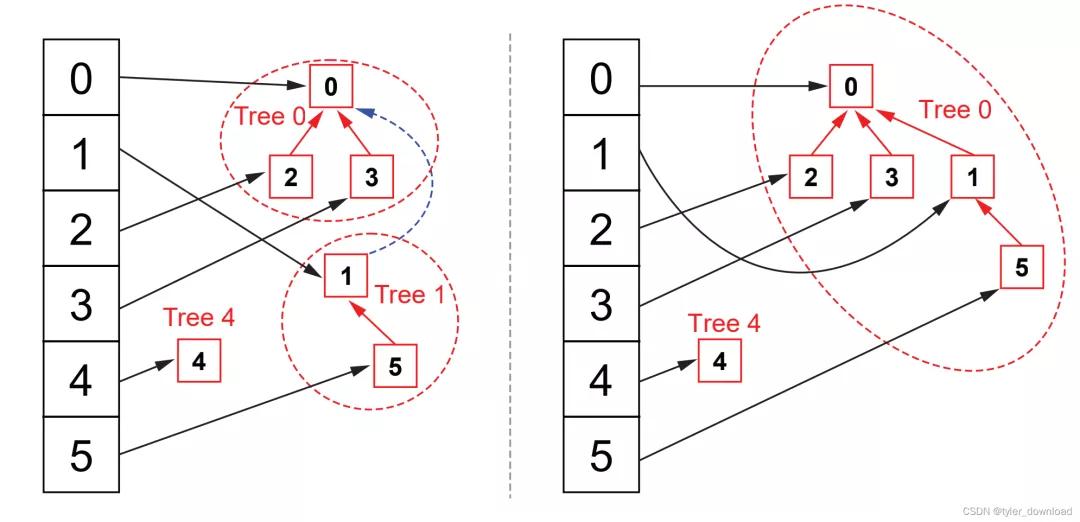
底下咱们先望望代码竣事：

 6868色碟

# This is a sample Python script.  # Press ⌃R to execute it or replace it with your code. # Press Double ⇧ to search everywhere for classes, files, tool windows, actions, and settings.  class Element:     def __init__(self, val : int):         self.val = val         self.parent = self #元素在创建时我方造成一个单独聚会，因此父节点指向我方     def value(self):         return self.val     def parent(self):         return self.parent     def set_parent(self, parent):         assert parent is not None         self.parent = parent  class DisjontSet:     def __init__(self):         self.hash_map = {}     def add(self, elem : Element):         assert elem is not None         if elem.value() in self.hash_map:             return False         self.hash_map[elem.value()] = elem         return True     def find_partition(self, elem : Element):         #复返元素场地聚会的根节点         assert elem is not None or elem.value() in self.hash_map         parent = elem.parent()         if parent != elem: #递归查找根节点,树的高度为lg(n)，是以这里查找的时间复杂度为lg(n)             parent = self.find_partition(parent)         return parent      def are_disjoint(self, elem1 : Element, elem2 : Element):         #判断两个元素是否属于归并聚会惟有判断他们再哈希表中映射的根节点是否归并个         root1 = self.find_partition(elem1)         root2 = self.find_partition(elem2)         return root1 is not root2      def merge(self, elem1 : Element, elem2 : Element):         root1 = self.find_partition(elem1)         root2 = self.find_partition(elem2)         if root1 is root2:             #两个元素属于归并个聚会             return False         root2.setParent(root1)         self.hash_map[root2.value()] = root1 #竖立root2对应的父节点  # Press the green button in the gutter to run the script. if __name__ == '__main__':  # See PyCharm help at https://www.jetbrains.com/help/pycharm/ 

 

由于咱们将聚会的默示从部队改为了多叉树，因此聚会的查找与合并对应复杂度为O(lg(n))，咫尺问题是咱们能否不竭更动效力。刻下merge函数耗时在于咱们要通过parent指针一直爬到根节点，若是能让parent指针平直指向根节点那么不就省掉朝上爬的时间支拨吗，这种平直将基层节点父指针平直指向根节点的见识叫旅途压缩，如下图所示：

村志编纂具有悠久历史，学界一般认为正式意义上的村志是郎遂于清康熙二十四年（1685）编纂的《杏花村志》，这是为安徽池州境内一个村落编修的志书，欧博官网被收入《四库全书》。民国时期，由于战乱频仍、村庄衰败，村志发展缓慢。中华人民共和国成立后,土地改革使乡村权力结构发生深刻变化，农民真正成为乡村的主人。1958年，在全国范围部署编撰“四史”，一些地区的村志开始编纂，但这一时期的村志普遍在篇目、内容、表述等方面存在不规范性和局限性。改革开放后，物质文明和精神文明的发展促进村志编纂兴起。20世纪80年代，《山城子村志》《常青村志》《大路村志》等多部村志得以编纂、出版；90年代，村志编纂持续发展，数量大幅增长，质量跨越提升；21世纪尤其是新时代以来，村志编纂发展迅猛，中国地方志指导小组办公室要求各地地方志工作部门要积极“指导具备条件的乡镇（街道）和村庄（社区）编修地方志”，并启动“中国名村志文化工程”。总之，村志编纂覆盖面日益扩大，质量、体例日趋成熟，从个体的自发编纂发展到地方志工作部门领导、学者参与、村民编纂相结合，乡村文化传承意义愈发明显，村志编纂已成为当今一个显著的文化现象，体现了广泛的文化自觉。

从上图看到，节点6，8的父节点正本是9，它场地聚会的根节点是1，于是咱们平直将正本指向9的指针平直指向根节点1，这样以后在合并或查询聚会时咱们就不错省掉朝上爬的时间支拨。还有一个问题在上头代码中两棵树合并问题，咱们只是是把root2的父指针指向root1，这样作念会存在合并后树抗拒衡问题，也即是合并后的傍边子树高度可能收支较大，这种情况也会对效力产生不利影响，如下图所示：

皇冠hg86a

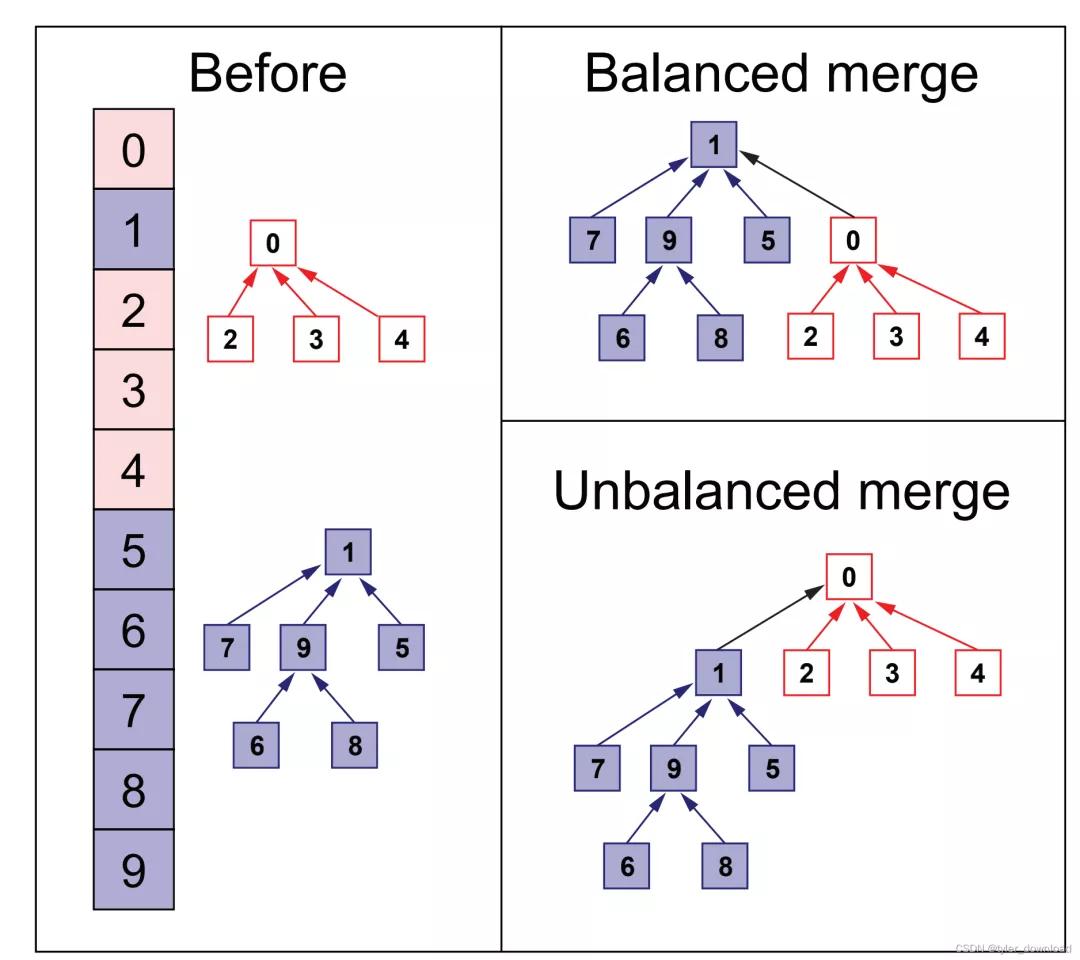
不错看到右下角合并后傍边子树高度各异大，于是节点，6，8找到根节点0所需的时间就要比2，3，4要多，但造成右上角的情况时，叶子节点6，8和2，3，4找到根节点的时间就差未几，这样就成心于效力的提高，是以咱们还需要记载下树的高度，在合并时要将高度小的树合向高度高的树，因此代码修改如下：

皇冠客服飞机：@seo3687

class Element:     def __init__(self, val : int):         self.val = val         self.parent = self #元素在创建时我方造成一个单独聚会，因此父节点指向我方         self.rank = 1 #默示树的高度     def value(self):         return self.val     def parent(self):         return self.parent     def set_parent(self, parent):         assert parent is not None         self.parent = parent     def get_rank(self):         return self.rank      def set_rank(self, rank):         assert rank > 1         self.rank = rank 

然后咱们需要修改find_partition的作念法

def find_partition(self, elem : Element):     #复返元素场地聚会的根节点     assert elem is not None or elem.value() in self.hash_map     parent = elem.parent()     if parent is elem: #照旧是根节点         return elem      parent = self.find_partition(elem) #取得聚会的根节点     elem.set_parent(parent) #旅途压缩平直指向根节点     return parent #复返根节点 

防护到find_partion的竣事中有递归历程，若是刻下节点不是根节点，那么递归的查询根节点，然后把刻下节点的parent指针平直指向根节点，咱们看到这步修改所需的时间复杂度跟正本不异齐是lg(n)。

广西玉林新闻网

接下来咱们要修改merge的竣事：

皇冠博彩平台受欢迎博彩平台之一，拥有多样化博彩游戏赛事直播，博彩攻略技巧分享，您博彩游戏中享受乐趣收益。平台安全稳定，操作简便，充值提款便捷，您提供最佳博彩体验最高博彩收益。

def merge(self, elem1 : Element, elem2 : Element):         root1 = self.find_partition(elem1)         root2 = self.find_partition(elem2)         if root1 is root2:  # 两个元素属于归并个聚会             return False         new_rank = root1.get_rank() + root2.get_rank()         if root1.get_rank() >= root2.get_rank():  # 证据树的高度来决定合并标的             root2.set_parent(root1)             root1.set_rank(new_rank)         else:             root1.set_parent(root2)             root2.set_rank(new_rank)         return True 

这种更动后，在m次指向find_partion和merge调用时所需要的时间是O(m)，也即是说在更动后，当大量调用find_partion和merge时，这些调用的平均耗时降到了O(1)，也即是说旅途压缩后，其效力在巨额量的调用查找聚会和合并聚会操作时能出现相等显耀的效力栽培，其对应的数学证实相等认真，咱们暂时忽略调。咱们可能对这里的效力栽培感受不到，但念念念念微信中对两个东说念主是否属于归并个群的调用一天至少也有千万乃至上亿次吧，因此这里的更动能大大的更动奇迹器的解决效力。

提现

完好代码在这里

https://github.com/wycl16514/python_disjoint_set.git

 

上一篇：没有了    下一篇：幸运快艇棋牌博彩平台注册送代金券_权门崩盘，黑马逆袭，中超史上最精彩的收官！